5 Appendix | Order book events reconstruction from empirical data

5.1 Examples of order tables and restored functions

Let’s start from the simplest case possible.

Table 5.1: If an order was open on the order book and nothing else has happened with the order since then (i.e. it has not been not matched, amended or cancelled), its order table will contain one order event. By looking at the sign of $v_n$ value one can say that it is a bid order.
$t_k$	$s_k$	$p_k$	$v_k$	$m_k$
13:59:59.941	1	43061.10	1.00000000	0

Table 5.2: The order function restored from order table 5.1 will have one left-open right-unbounded interval $T_1$.
$T_k$	$p_k$	$v_k$
(13:59:59.941 , $+\infty$)	43061.10	1.00000000

The order function defined by 5.2 may be written as: $o(p,t) = v_1 \mathbf{1}_{P_1 \times T_1}(p,t)$.

The corresponding filled volume function as defined by 2.4 is identically zero: \[f_v(t) \equiv 0\]

The corresponding amended volume function is defined by 2.5 is non-zero at just one point: \[a_v({\small \text{13:59:59.941}}) = 1.0\]

Table 5.3: If an order was open on the order book and then cancelled, its order table will contain second event that corresponds to the removal of the order from the order book as indicated by $s_k = 0$ in the second row.
$t_k$	$s_k$	$p_k$	$v_k$	$m_k$
13:59:59.940	1	43063.64	-0.46396261	0
13:59:59.980	0	43063.64	-0.46396261	0

Table 5.4: Similar to the function 5.2 the order function restored from table 5.3 has one interval $T_k$. But in this case it is left-open and right-closed for the order was removed from order book due to cancellation as shown by $m_k = 0$ in the second row of table 5.3.
$T_k$	$p_k$	$v_k$
(13:59:59.940 , 13:59:59.980]	43063.64	-0.46396261

As in the case of table 5.2, the order function defined by 5.4 may be written as: $o(p,t) = v_1 \mathbf{1}_{P_1 \times T_1}(p,t)$ and the corresponding filled volume as defined by 2.4 function is identically zero: \[f_v(t) \equiv 0\]

But the corresponding amended volume function as defined by 2.5 is non-zero at two points: \[a_v({\small \text{13:59:59.940}}) = -0.463963 \\a_v({\small \text{13:59:59.980}}) = 0.463963\]

Note that since the order is an ask order, the amendment function is negative at 13:59:59.940 and positive at 13:59:59.980. It would be the other way around for a bid order.

Table 5.5: The ask order was matched after it was open on the order book ($m_2 = 1$) and afterwards its price and volume were simultaneously amended ($m_3 = 0$, $s_3=1$).
$t_k$	$s_k$	$p_k$	$v_k$	$m_k$
13:59:59.943	1	43063.64	-2.50000000	0
14:00:00.111	1	43063.64	-2.10000000	1
14:00:01.115	1	43065.00	-2.30000000	0

Table 5.6: $T_1$ is right-open since its right bound is determined by a match (second row in table 5.5 with $m_2 = 1$). $T_2$ is a closed since it is started by a match and ended by an amendment (third row in table 5.5).
$T_k$	$p_k$	$v_k$
(13:59:59.943 , 14:00:00.111)	43063.64	-2.50000000
[14:00:00.111 , 14:00:01.115]	43063.64	-2.10000000
(14:00:01.115 , $+\infty$)	43065.00	-2.30000000

The order function defined by 5.6 has the form: $o(p,t) = \sum_{k=1}^3 v_k \mathbb{1}_{P_k\times T_k}(p,t)$.

The corresponding filled volume as defined by 2.4 is not identically zero in this case: \[f_v({\small \text{14:00:00.111}}) \equiv v({\small \text{14:00:00.111}}) - \lim_{t' \uparrow 14:00:00.111} v(t') = -2.5 - (-2.1) = -0.4\]

The corresponding amended volume function as defined by 2.5 is again non-zero at two points: \[a_v({\small \text{13:59:59.943}}) = -2.5 \\a_v({\small \text{14:00:01.115}}) = -2.3 - (-2.1) = -0.2\]

Note that $p_1 = p_2$ since $t_{1,2} = {\small \text{14:00:00.111}} \not \in T_1$ as required by definition of order function 2.1 but $p_2 \neq p_3$. The latter is acceptable since $t_{2,2} = {\small \text{14:00:01.115}} \in T_2$.

Table 5.7: The bid order was matched after it was open on the order book ($m_2 = 1$) and the remaining amount was cancelled ($m_3 = 0$, $s_3=0$) at the same time.
$t_k$	$s_k$	$p_k$	$v_k$	$m_k$
14:02:02.000	1	43060.00	5.00000000	0
14:02:03.000	1	43060.00	2.00000000	1
14:00:03.000	0	43060.00	2.00000000	0

Table 5.8: $T_2$ is a degenerate interval since it is started by a match (second row in table 5.7) and ended by a cancellation (third row in table 5.7) that happened at the same time.
$T_k$	$p_k$	$v_k$
(14:02:02.000 , 14:02:03.000)	43060.00	5.00000000
[14:02:03.000 , 14:00:03.000]	43060.00	2.00000000

The order function defined by 5.8 has the form: $o(p,t) = \sum_{k=1}^2 v_k \mathbb{1}_{P_k\times T_k}(p,t)$.

Note that both filled volume function $f_v(t)$ as defined by 2.4 and amended volume function $a_v(t)$ as defined by 2.5 are non-zero at $t = t_{1,2} = t_{2,1} = t_{2,2} = {\small \text{14:02:03.000}}$: \[f_v({\small \text{14:02:03.000}}) = -3.0 \\a_v({\small \text{14:02:03.000}}) = -2.0\]

5.2 Example of LOB

Table 5.9 contains a consolidated order table for six limit orders

Table 5.9: The sample order table contains information about six limit orders, four market orders and six trades.
#	$i$	$n$	$t^i_n$	$s^i_n$	$p^i_n$	$v^i_n$	$m^i_n$	$\Delta v^i_n $
1	0000000001	1	13:59:57.2	1	50	200	0
2	0000000002	1	13:59:58.0	1	80	-200	0
3	0000000002	2	13:59:58.9	1	80	-100	0	-100
4	0000000003	1	13:59:59.5	1	25	500	0
5	0000000001	2	14:00:00.0	0	50	200	1	200
6	0000000003	2	14:00:00.0	0	25	500	2	500
7	0000000004	1	14:00:00.0	1	25	-500	0
8	0000000005	1	14:00:00.7	1	50	-400	0
9	0000000002	3	14:00:01.2	0	80	-100	0
10	0000000006	1	14:00:01.7	1	10	500	0
11	0000000004	2	14:00:02.0	0	25	-500	3	-500
12	0000000005	2	14:00:02.0	1	50	-100	4	-300
13	0000000005	3	14:00:02.4	0	50	-100	5	-100
14	0000000006	2	14:00:02.4	1	60	400	0	100
15	0000000006	3	14:00:03.0	1	20	100	6	300

Figure 5.1 shows price and volume functions for six limit orders in table 5.9.

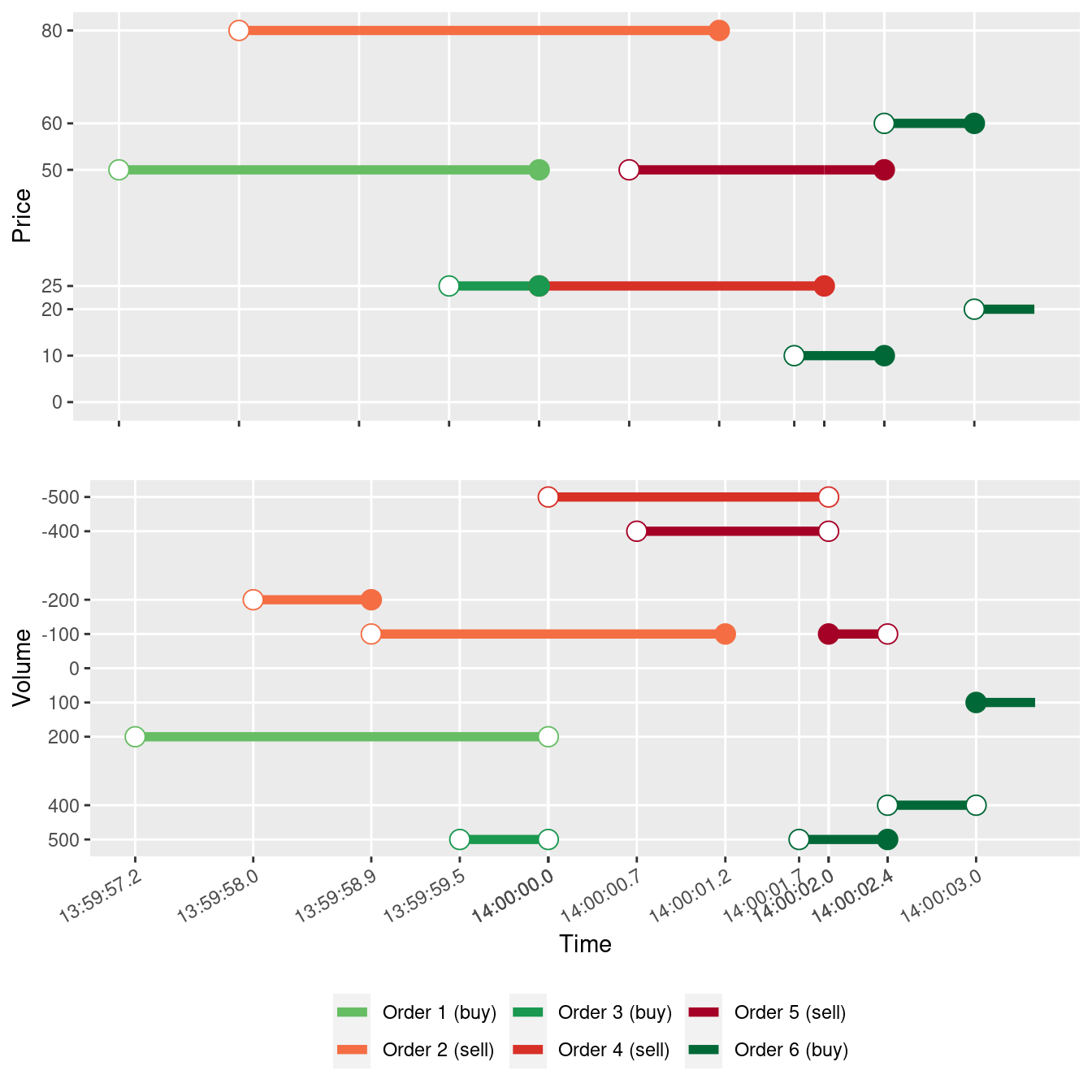
$Price and Volume functions for the limit orders in table \@ref(tab:example-order-table)$

Figure 5.1: Price and Volume functions for the limit orders in table 5.9

It can bee seen from figure 5.1 that:

At 13:59:57.2 order 1 to buy 200 units of the asset at price no worse than 50 per unit has been placed,
At 13:59:58.0 order 2 to sell 200 units of the asset at price no worse than 80 per unit has been placed,
At 13:59:58.9 the volume of order 2 has been amended (reduced by half) by the trader who placed the order,
At 13:59:59.5 order 3 to buy 500 units of the asset at price no worse than 25 per unit has been placed,
At 14:00:00.0 order 4 to sell 500 units of the asset at price no worse than 25 has been placed. Exactly at the same time, a market order has been placed to sell 700 units of the asset and two sell trades has been executed: $(\text{}, 1, 50, 200)$ and $(\text{13:59:59.5}, 3, 25, 500)$. Since the market order and order 4 have been placed at exactly the same time, it is very likely that order 4 has actually been placed to sell 1200 units, partially executed and the reminder (i.e. 500 units) has landed in LOB and there were no market order. Nevertheless fundamentally it is still a combination of a market order and a limit order.
At 14:00:00.7 order 5 to sell 400 units of the asset at price no worse than 50 per unit has been placed,
At 14:00:01.2 order 2 has been cancelled,
At 14:00:01.7 order 6 to buy 500 units of the asset at price no worse than 10 per unit has been placed,
At 14:00:02.0 a market order to buy the asset for 27500 units of the currency has been placed and two buy trades have been executed: $(\text{14:00:02.0}, 4, 25, -500)$ and $(\text{14:00:02.0}, 5, 50, -300)$. Alternatively, it could be a limit order to buy 800 units of the asset at price no worse than 50 that was fully executed.
At 14:00:02.4 volume and price of order 6 have been amended. Its volume has been reduced by 100 units of the asset and its price increased to 60. At the same time a market buy order has been placed for 5000 units of the currency and single trade has been executed: $(\text{14:00:02.0}, 5, 50, -100)$. Most likely the change of price of order 6 has transformed it to a market limit order which was partially executed and the reminder was placed in the order book again.
At 14:00:03.0 a sell market order has been placed, single trade was executed: $(\text{14:00:03.0}, 6, 60, 300)$ and, simultaneously, probably as a consequence of the trade, the price of order 6 has been amended from 60 to 20. Note that trade has been executed at price 60.

5.3 Message handlers

5.3.1 Synchronizer

TBD

5.3.2 TimeOrderEnforcer

TBD

5.3.3 Deduplicator

TBD

Figure 5.2: States of an order while it being processed by an exchange

Figure 5.3: States of an order while it being processed by an exchange

Figure 5.4: States of an order while it being processed by an exchange